Optic Flow

For many tasks in the area of image processing and computer vision a fast and accurate computation of the results is required. One may claim that the rapid progress in the sector of computer engineering will solve this problem by allowing algorithms to become faster year by year. However, these accelerations are rather small compared to those obtained by state-of-the-art numerical methods.

Our research in the area of scientific computing includes a variety of topics:

• Multigrid Methods
  Multigrid methods are well-known to be among the fastest and most accurate numerical schemes for the solution of linear and nonlinear system of equations. By creating a sophisticated coarse to fine hierarchy starting from the original equation system they offer much better error reduction properties than frequently used non-hierarchical solvers. Thus very accurate results are already obtained within a few iterations. In [1,2] we developed such multigrid schemes for the purpose of real-time optic flow estimation. As a result up to 42 dense flow fields of size 200 x 200 could be computed on a standard desktop PC within a single second. Compared to the frequently used Gauss--Seidel method this equals an acceleration of two to three orders of magnitude.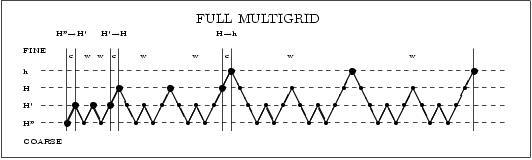
  

• Splitting Schemes
  A second numerical approach for the acceleration of algorithms is the use of so called splitting schemes. They allow for a decomposition of a single problem into multiple problems that offer certain advantages compared to the original one. In general, the resulting problems can be solved very efficiently with standard numerical methods. Some of them even offer advantages regarding a possible parallelisation. Our research mainly focuses on additive operator splitting (AOS) schemes, which have the advantage of being rotationally invariant compared to their multiplicative counterparts. In [3] such an AOS scheme is presented for the first time to the image processing and computer vision community. Apart from nonlinear diffusion filtering, variants for regularisation methods [4] and optic flow computation [5] have been developed. Recently, we also used AOS schemes successfully in the context of active contour models [6].

• Parallel Computing
  For certain problems the use of sophisticated numerical schemes may still not be enough to obtain the desired performance. At this point, one should consider the use of high performance cluster systems. In many cases, the parallelisation of fast sequential algorithms is a very challenging task. In [7,8,9] we present some parallelisation strategies for a nonlinear diffusion filter that is based on a highly efficient additive operator splitting (AOS) scheme. Using the inter-process communication standard MPI the implemented algorithm showed an excellent scaling behaviour with speed up factors of up to 209 for 256 processors. The research on this topic is in cooperation with the Computer Architecture Group at the University of Mannheim in Germany.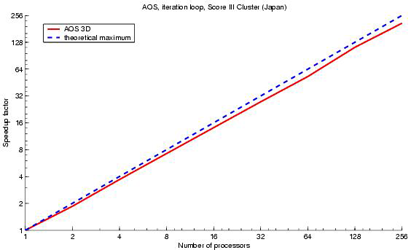
  

• Domain Decomposition Methods
  Domain decomposition is a frequently used strategy for parallelizing linear and nonlinear system of equations. Thereby the original problem is divided in sub-domains, for which the problem is solved locally. From time to time boundaries are updated by solving additional equation systems that take the global context into consideration. In [10,11,12] we have developed such domain decomposition strategies for parallel computation of optic flow fields. The research on this topic is in cooperation with the Computer Vision, Graphics and Pattern Recognition Group at the University of Mannheim in Germany.

1. A. Bruhn, J. Weickert, C. Feddern, T. Kohlberger and C. Schnörr:
   Real-time optic flow computation with variational methods.
   In N. Petkov, M. A. Westenberg (Eds.), Computer Analysis of Images and Patterns. Lecture Notes in Computer Science, Vol. 2756, Springer, Berlin, 222-229, 2003.
   

2. A. Bruhn, J. Weickert, C. Feddern, T. Kohlberger, C. Schnörr:
   Variational optic flow computation in real-time.
   IEEE Transactions in Image Processing, to appear.
   Revised version of Technical Report No. 89, Department of Mathematics, Saarland University, Saarbrücken, Germany, June 2003.
   

3. J. Weickert, B.M. ter Haar Romeny, M.A. Viergever:
   Efficient and reliable schemes for nonlinear diffusion filtering.
   IEEE Transactions on Image Processing, Vol. 7, 398-410, 1998.
   

4. J. Weickert:
   Efficient image segmentation using partial differential equations and morphology.
   Pattern Recognition, Vol. 34, No. 9, 1813-1824, September 2001.
   Also available as Technical Report No. 3/2000. Computer Science Series, University of Mannheim, Germany, February 2000.
   

5. J. Weickert, C. Schnörr:
   Variational optic flow computation with a spatio-temporal smoothness constraint.
   Journal of Mathematical Imaging and Vision, Vol. 14, No. 3, 245-255, May 2001.
   Revised version of Technical Report No. 15/2000. Computer Science Series, University of Mannheim, Germany, July 2000.
   

6. J. Weickert, G. Kühne:
   Fast methods for implicit active contour models.
   In S. Osher, N. Paragios (Eds.): Geometric Level Set Methods in Imaging, Vision and Graphics. Springer, 2003.
   

7. A. Bruhn, T. Jakob, M. Fischer, T. Kohlberger, J. Weickert, U. Brüning, C. Schnörr:
   Designing 3-D nonlinear diffusion filters for high performance cluster computing.
   In L. Van Gool (Ed.): Pattern Recognition. Lecture Notes in Computer Science, Vol. 2449, Springer, Berlin, 290-297, 2002.

8. D. Slogsnat, M. Fischer, A. Bruhn, J. Weickert, U. Brüning:
   Low level parallelization of nonlinear diffusion filtering algorithms for cluster computing environments.
   In H. Kosch, L. Böszörményi, H. Hellwagner (Eds.): Euro-Par 2003. Parallel Processing. Lecture Notes in Computer Science, Vol. 2790, Springer, Berlin, 481-490, 2003.
   

9. A. Bruhn, T. Jakob, M. Fischer, T. Kohlbeger, J. Weickert, U. Brüning, C. Schnörr:
   High performance cluster computing with 3-D nonlinear diffusion filters.
   Real-Time Imaging, Vol. 10, No. 1, 41-51, 2004.
   Revised version of Technical Report No. 87, Department of Mathematics, Saarland University, Saarbrücken, Germany, 2003.
   

10. T. Kohlberger, C. Schnörr, A. Bruhn, J. Weickert:
    Domain decomposition for parallel variational optic flow computation.
    In B. Michaelis, G. Krell (Eds.): Pattern Recognition. Lecture Notes in Computer Science, Vol. 2781, Springer, Berlin, 196-202, 2003.
    

11. T. Kohlberger, C. Schnörr, A. Bruhn, J. Weickert:
    Parallel variational motion estimation by domain decomposition and cluster computing..
    In T. Pajdla, J. Matas (Eds.): Computer Vision - ECCV 2004. Lecture Notes in Computer Science, Vol. 3024, Springer, Berlin, 205-216, 2004.

12. T. Kohlberger, C. Schnörr, A. Bruhn, J. Weickert:
    Domain decomposition for variational optical flow computation..
    IEEE Transactions in Image Processing, to appear.
    Revised version of Technical Report 2003/7, Computer Science Series, University of Mannheim, May 2003.

MIA Group
©2001-2005
The author is not
responsible for
the content of
external pages.