Semidiscrete Analysis and Numerics of Diffusion Processes

The aim of this work is firstly to model and analyse numerical schemes for diffusion filtering PDEs of image analysis, for example with respect to their stability and convergence properties.

A particularly fruitful direction in this context is the investigation of ODE systems which describe spatially discretised image filters with continuous (time or scale) parameter. Often these systems have discontinuous right-hand sides.

Furthermore, it is possible in this way to obtain novel, theoretically well-founded methods with designed properties.

• Novel numerical algorithms for isotropic nonlinear diffusion filters with applications in image analysis could be developped that combine advantageous stability properties with extraordinarily low numerical dissipation. In particular, these approaches allow to handle singular diffusion processes like total variation methods without resorting to a regularisation by bounding the diffusivities. Such a regularisation is commonly used but interferes with the favourable properties of the filtering process [1, 2, 3, 4, 7].
  
  
  
  
• Similar numerical algorithms could be derived for anisotropic nonlinear diffusion filters [5, 7].
• Space-discrete analysis of staircasing effects occurring in inverse diffusion filters in 1D [6].
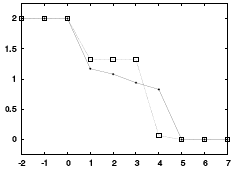
• Stability analysis for discrete Forward-and-Backward (FAB) diffusion, a nonlinear diffusion model with positive and negative diffusivities [8].

1. P. Mrázek, J. Weickert, G. Steidl, M. Welk:
   On iterations and scales of nonlinear filters.
   In O. Drbohlav (Ed.): Computer Vision Winter Workshop 2003, Valtice, Czech Republic, 61-66. Czech Pattern Recognition Society, 2003.
   
2. G. Steidl, J. Weickert, T. Brox, P. Mrázek and M. Welk:
   On the equivalence of soft wavelet shrinkage, total variation diffusion, total variation regularization, and SIDEs.
   SIAM Journal on Numerical Analysis, Vol. 42, No. 2, 686-713, 2004.
   An extended version appeared as Technical Report No. 94, Department of Mathematics, Saarland University, Saarbrücken, Germany, August 2003.
   
3. M. Welk, J. Weickert, G. Steidl:
   A four-pixel scheme for singular differential equations.
   In R. Kimmel, N. Sochen, J. Weickert (Eds.): Scale-Space and PDE Methods in Computer Vision. Lecture Notes in Computer Science, Vol. 3459, Springer, Berlin, 610–621, 2005.
   

4. J. Weickert, G. Steidl, P. Mrázek, M. Welk, T. Brox:
   Diffusion filters and wavelets: What can they learn from each other?
   In N. Paragios, Y. Chen, O. Faugeras (Eds.): Handbook of Mathematical Models in Computer Vision. 3-16, Springer, New York, 2006.
   Also available as Preprint No. 77, DFG Priority Programme 1114, University of Bremen, Germany, January 2005.
   
5. M. Welk, J. Weickert, G. Steidl:
   From tensor-driven diffusion to anisotropic wavelet shrinkage.
   In H. Bischof, A. Leonardis, A. Pinz (Eds.): Computer Vision – ECCV 2006. Lecture Notes in Computer Science, Vol. 3951, 391–403. Springer, Berlin, 2006.
   

6. M. Breuß, M. Welk:
   Staircasing in semidiscrete stabilised inverse diffusion algorithms.
   Journal of Computational and Applied Mathematics, Vol. 206, No. 1, 520-533, 2007.
   Revised version of Technical Report No. 165, Department of Mathematics, Saarland University, Saarbrücken, Germany, January 2006.
   
7. M. Welk, G. Steidl, J. Weickert:
   Locally analytic schemes: a link between diffusion filtering and wavelet shrinkage.
   Applied and Computational Harmonic Analysis, Vol. 24, 195–224, 2008.
8. M. Welk, G. Gilboa, J. Weickert:
   Theoretical foundations for discrete forward-and-backward diffusion filtering.
   To appear in Proc. Second International Conference on Scale-Space and Variational Methods (SSVM 2009, Voss, Norway, June 2009).

Martin Welk/12 January 2010

MIA Group
©2001-2023
The author is not
responsible for
the content of
external pages.

Imprint - Data protection