Halftoning

Many devices such as printers and fax machines can often create only pure black and white images. To represent intermediate grey values, it is necessary to virtually increase the range of such devices by using a halftoning algorithm.
Halftoning algorithms can be divided into two classes: Dithering algorithms, which use square-shaped black and white dots located on a regular grid (see middle image), and stippling algorithms which place round dots at arbitrary positions (see right image). In our work, we have developed algorithms for both classes.

Input image	Dithering result	Stippling result

Lattice-Boltzmann Model

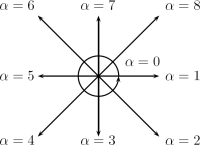
Encoding of directions in LB framework

Our first contribution [1] is an iterative dithering algorithm by use of a lattice Boltzmann framework. Lattice Boltzmann methods have been introduced as an alternative numerical method for simulating fluid dynamics. In our approach we assume that grey values are small particles. Lattice Boltzmann models are able to model transitions between discrete grid points in an iterative scheme on a microscopic level that effect the result on a macroscopic level.

Our transitions are based on local gradients such that we allow a flow of particles towards pixels with higher grey value and block flow in opposite direction. With this setting it is possible to bring pixels to desirable states such as black or white states. After convergence of the iterative scheme we perform a thresholding for pixels that were not binarised.

Original image	Dithering with Floyd-Steinberg (1976)	Dithering with lattice Boltzmann model

By construction of this framework, we are able to give an iterative rotationally invariant dithering algorithm. Furthermore, the embedding into the lattice Boltzmann framework allows to derive a macroscopic formulation, from which follows that our method employs a diffusion-advection equation.
Our model is able to give a contrast-enhancing dithering result that is rotationally invariant and does not rely on sweeping directions or arbitrary pixel stencils.

Electrostatic Halftoning

Our halftoning approach in [2] models black dots in the image by charged particles which repel each other, but are attracted by grey values in the image. It is motivated by the fact that, for regions of constant density, e.g. regions of constant grey value in an image, black points in the resulting image shall be equally distributed.

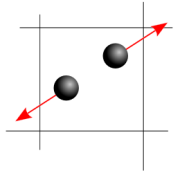
Repulsion between particles

First, let us focus on a uniform grey image. We initialise the solution with a random distribution of the desired number of black pixels. Next, we regard these pixels as small charged particles within a 2-D particle system on a bounded domain. As a consequence of electrostatic laws, these particles repulse each other. If we simulate the evolution of the system for some time, particles will move such that their relative distances are maximised. In the end, this gives us a uniform distribution of particles in the specified domain: We obtain a halftoned image.

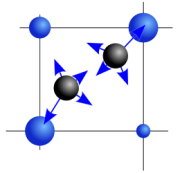
Attraction by grid points

The system described so far cannot create halftones of images with more than one grey value. However, this drawback can easily be remedied: At all grid positions, we introduce stationary charges that are proportional to the grey value of the respective pixel of the input image. These "invisible" particles attract moving charges and thus control the number of black pixels within any region.

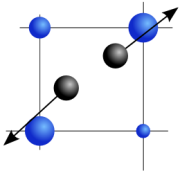
Resulting forces on particles

Finally, we regard both attractive and repulsive forces during the evolution of the image. This yields an appealing halftoning result where both constant regions and edges in the image are synthesised. Since the overall system is designed to be electrically neutral, it allows a a precise reproduction of all grey values in both dithering and stippling applications.
Several extensions of this intuitive and flexible halftoning approach are explained in our paper [2] and at our supplementary material page, which also contain detailed evaluations and comparisons against other state-of-the-art algorithms. Our paper [3] presents a more detailed mathematical analysis as well as an asymptotically faster minimisation approach that is based on non-equispaced fast Fourier transforms (NFFTs). In [4], we introduce a fast parallel GPU-based NFFT algorithm, which yields the same high quality as in [2] in a fraction of the original runtime. We also extended our approach such that it can handle dots with arbitrary colours and sizes, yields an improved rendering of saturated image areas, can perform multi-class sampling, and can create hatched images. Details about these extensions can be found in [5].

1. K. Hagenburg, M. Breuß, O. Vogel, J. Weickert, M. Welk:
   A lattice Boltzmann model for rotationally invariant dithering.
   In G. Bebis, R. Boyle, B. Parvin, D. Koracin, Y. Kuno, J. Wang, R. Pajarola, P. Lindstrom, A. Hinkenjann, M. L. Encarnaçao, C. T. Silva, D. Coming (Eds.): Advances in Visual Computing. Lecture Notes in Computer Science, Vol. 5876, 949-959, Springer, Berlin, 2009


2. C. Schmaltz, P. Gwosdek, A. Bruhn, J. Weickert:
   Electrostatic halftoning.
   Computer Graphics Forum, Vol. 29, No. 8, 2313-2327, December 2010.
   Revised version of Technical Report No. 260, Department of Mathematics, Saarland University, Saarbrücken, Germany, February 2010.
   See also: Supplementary Material Webpage.


3. T. Teuber, G. Steidl, P. Gwosdek, C. Schmaltz, J. Weickert:
   Dithering by differences of convex functions.
   SIAM Journal on Imaging Sciences, Vol. 4, No. 1, 79-108, January 2011.
   Revised version of Technical Report No. Pr-2010-01, Department of Mathematics, University of Mannheim, Germany, April 2010.


4. P. Gwosdek, C. Schmaltz, J. Weickert, T. Teuber:
   Fast electrostatic halftoning.
   Journal of Real-Time Image Processing, Vol. 9, No. 2, 379-392, June 2014.
   Revised version of Technical Report No. 295, Department of Mathematics, Saarland University, Saarbrücken, Germany, June 2011.


5. C. Schmaltz, P. Gwosdek, J. Weickert:
   Multi-class anisotropic electrostatic halftoning.
   Computer Graphics Forum, Vol. 31, No. 6, 1924-1935, Sept. 2012.
   Revised version of Technical Report No. 301, Department of Mathematics, Saarland University, Saarbrücken, Germany, October 2011.
   See also: Supplementary Material Webpage.

MIA Group
©2001-2023
The author is not
responsible for
the content of
external pages.

Imprint - Data protection