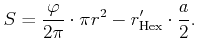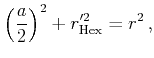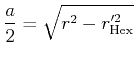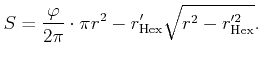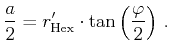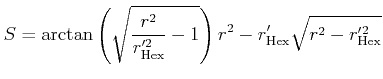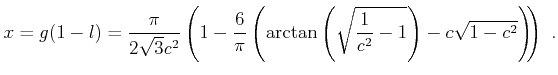Multi-Class (Anisotropic) Electrostatic Halftoning - Mathematical Image Analysis Group, Saarland University

Multi-Class (Anisotropic) Electrostatic Halftoning
Deviation of Tonemapping Operator

Using our basic halftoning algorithm, the total area of all dots inside a certain region equals the (scaled) sum of the grey values of that region. In very dark image regions, however, the dots will overlap. Thus, these regions are rendered brighter than they should be. On this page, we derive the equations necessary to compute the tonemapping operator that should be applied before halftoning to account for this overlap.
First, we let us analyse how large the overlapping regions are. For this, we assume that the particles are aligned in an energetically optimal honeycomb pattern in an area of constant grey value. We note that overlaps occur only if the circular disc that represents a particle is larger than the incircle of the corresponding hexagons. Using the notation from the images shown below, this is the case if $r > r_\mathrm{Hex}'$ . If it equals the circumcircle, the area is rendered in a fully black tone.

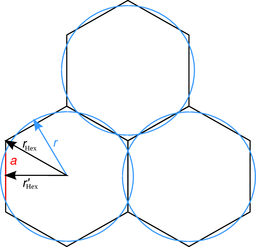
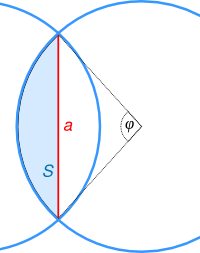
Illustration of the identifiers used on this page.
Blue: Particles forming an energetically optimal honeycomb pattern. Black: Underlying hexagons.
Left: Overlap of particles in a honeycomb pattern. Right: Zoom on one overlap area.

First of all, let us compute the grey value corresponding to the borderline case $r = r_\mathrm{Hex}'$ . This is done by computing the coverage in this situation: We consider the triangle between the centres of three neighbouring circles and denote its height by

. Then, its areas is given by $A_\Delta := \frac12 (2r) h = \sqrt3 r^2$ . Within this triangle, there are three sectors of $\frac16$ the area of a circle, each. The coverage in this case is thus given by:

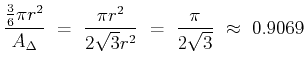$\displaystyle \frac{\frac36 \pi r^2}{A_\Delta} \ =\ \frac{\pi r^2}{2\sqrt3 r^2} \ =\ \frac{\pi}{2\sqrt3} \ \approx\ 0.9069$

(1)

Consequently, above a grey value of

, the circles do not overlap.

In the interesting case $r > r_\mathrm{Hex}'$ , we can express the circular segment

cut off by

as the difference between the circular sector spanned by $\varphi$ and the triangle, i.e.

$\displaystyle S = \frac\varphi{2\pi} \cdot \pi r^2 - r_\mathrm{Hex}' \cdot \frac a2.$

(2)

$\displaystyle \left(\frac a2\right)^2 + r_\mathrm{Hex}'^2 = r^2 ,$

(3)

$\displaystyle \frac a2 = \sqrt{r^2 - r_\mathrm{Hex}'^2}$

(4)

$\displaystyle S = \frac\varphi{2\pi} \cdot \pi r^2 - r_\mathrm{Hex}' \sqrt{r^2 - r_\mathrm{Hex}'^2}.$

(5)

$\displaystyle \frac a2 = r_\mathrm{Hex}' \cdot \tan \left(\frac \varphi2\right) .$

(6)

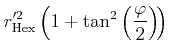		$\displaystyle r_\mathrm{Hex}'^2 \left(1 + \tan^2\left(\frac\varphi2\right)\!\right)$	$\displaystyle =r^2$	(7)
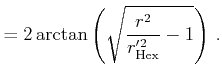$\displaystyle \Rightarrow$		$\displaystyle \varphi$	$\displaystyle = 2 \arctan\left(\sqrt{\frac{r^2}{r_\mathrm{Hex}'^2} - 1}\right) .$	(8)

$\displaystyle S = \arctan\left(\sqrt{\frac{r^2}{r_\mathrm{Hex}'^2} - 1}\right) r^2 - r_\mathrm{Hex}' \cdot \left(\sqrt{r^2 - r_\mathrm{Hex}'^2}\right)$

(9)

Let us now express the total overlap

relative to the area of one circle, and call this the relative loss

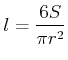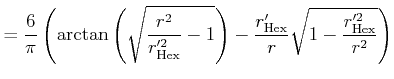$\displaystyle l = \frac{6S}{\pi r^2}$	$\displaystyle = \frac6\pi \left(\arctan\left(\sqrt{\frac{r^2}{r_\mathrm{Hex}'^2... ...{Hex}'}r \cdot \left(\sqrt{1 - \frac{r_\mathrm{Hex}'^2}{r^2}}\right)\!\!\right)$	(10)
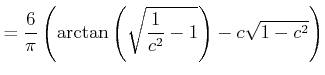	$\displaystyle = \frac6\pi \left( \arctan \left( \sqrt{\frac1{c^2} - 1}\right) - c \sqrt{1 - c^2}\right)$	(11)

Note that we substitute $\frac{r_\mathrm{Hex}'}r =: c$ . This makes sense since

is a free parameter and $r_\mathrm{Hex}'$ depends on

and on the grey value of the image. The ratio

thus allows us to regard the problem independent of the scale, i.e. the absolute error.

Let us forget the loss for a moment and consider the case $r \leq r_\mathrm{Hex}'$ in which the rendering works as expected. Here, we obtain the grey value

as the quotient of the area of the circular disc and the hexagon it covers:

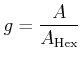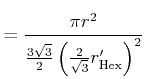$\displaystyle g = \frac{A}{A_\mathrm{Hex}}$	$\displaystyle \overset{\eqref{eq:proof.halftoning.areahex}}= \frac{\pi r^2}{\frac{3\sqrt3}2\left(\frac2{\sqrt3} r_\mathrm{Hex}'\right)^2}$	(12)
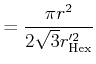	$\displaystyle = \frac{\pi r^2}{2\sqrt3 r_\mathrm{Hex}'^2}$	(13)
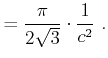	$\displaystyle = \frac\pi{2\sqrt3} \cdot \frac1{c^2} .$	(14)

If the rendering worked well in dark areas, we would also expect such

in these cases. In other words, the relative loss

just describes the deviation of the true grey value

from the desired grey value

. The relative remainder

thus denotes the fraction of the area that is still rendered. Since the area and the grey value depend linearly on each other, we can express

$\displaystyle x = g(1 - l) = \frac\pi{2\sqrt3} \cdot \frac1{c^2} \cdot \left(1 ... ...an \left( \sqrt{\frac1{c^2} - 1}\right) - c \sqrt{1 - c^2}\right)\!\!\right) .$

(15)

At this point, we can switch the roles of action and reaction: Considering a certain grey value

shall be obtained, which grey value

would we need to sample? Since (15) depends only on

and

, we can solve it numerically for

assuming a desired

. Since the function is not monotonic, we can use that we are only interested in

	$\displaystyle r_\mathrm{Hex}' \hspace{-1.85cm}$	$\displaystyle \leq r \hspace{-1.85cm}$	$\displaystyle \leq r_\mathrm{Hex}$	(16)
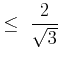$\displaystyle \Leftrightarrow$	$\displaystyle \qquad1 \hspace{-1.85cm}$	$\displaystyle \leq \frac1c \hspace{-1.85cm}$	$\displaystyle \leq \frac2{\sqrt3}$	(17)
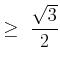$\displaystyle \Leftrightarrow$	$\displaystyle \qquad1 \hspace{-1.85cm}$	$\displaystyle \geq c \hspace{-1.85cm}$	$\displaystyle \geq \frac{\sqrt3}2$	(18)

Finally, we use

in (14) to obtain

. To finish this derivation, let us check the global mass preservation of the process given that a tonemapping as explained in the paper is applied. Regions with a grey value below $\frac\pi{2\sqrt3}$ are rendered correctly, since

. Above this threshold, the grey value preservation follows by construction from (14) and (15).