Complementary Optic Flow on GPU - Mathematical Image Analysis Group, Saarland University

Complementary Optic Flow on the GPU

Numerics
Fast Explicit Diffusion (FED)

Like all variational approaches, our model requires the solution of huge systems of equations to obtain an optimal solution. Consequently, this part typically constitutes the most expensive part of the algorithm and is thus crucial for its overall run-time.

Thus, we use a solver recently proposed by Grewenig et al. [1]. This so-called Fast Explicit Diffusion (FED) is a general-purpose solver for diffusion-like processes. It is based on an explicit scheme, but uses varying mathematically founded time steps. About half of them exceed the stability bound for explicit schemes, while the other half is below this limit. By this construction, one can show unconditional stability for the whole process.

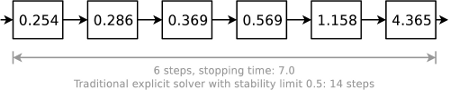
A stable series of steps forms one linear cycle with a certain stopping time. If one considers a non-linear problem (like our optic flow approach), these cycles can easily be combined with a lagged diffusivities framework: To ensure stability, the update of the diffusivity or the diffusion tensor is only implemented at the beginning of each cycle.

In order to accelerate the convergence of this process even further, we embed our FED solver in a coarse-to-fine strategy. This means, we first recursively compute the solution for a downsampled version of the problem, and use the upsampled solution as an initialisation for the next finer level.

With these simple ingredients — a basic explicit solver within a coarse-to-fine strategy — we obtain framerates comparable to those of modern bi-directional full multigrid (FAS) solvers. Still, the effort to implement this framework is fairly moderate on both a CPU and a GPU.

A library that computes the specific step sizes for FED is available as free software and can be downloaded on our research pages.

References:

[1] S. Grewenig, J. Weickert, A. Bruhn:
From box filtering to fast explicit diffusion.
In Pattern Recognition, Proc. 32th DAGM Symposium
DAGM 2010, Darmstadt, Germany, September 2010.
Lecture Notes in Computer Science, Vol. 6376, 533-542, Springer, Berlin, 2010.

< Model Main Page Results with GT >